Spanish Vowels
Like in English, Spanish vowels are essential for forming words and sentences.
They’re also commonly pronounced incorrectly by Spanish learners.
While they look the same as our English vowels (a, e, i, o, u and sometimes y), they’re pronounced differently.
In this post, you’ll learn all about Spanish vowels and their pronunciations.
You’ll also get to know vowel combinations called diphthongs, triphthongs and hiatuses in Spanish, with plenty of examples for you to see them in action.
Contents
- The Basics of Spanish Vowels
- Tips for Pronouncing Spanish Vowels
- Pronouncing Spanish Vowel Combinations
- And One More Thing…
Download: This blog post is available as a convenient and portable PDF that you can take anywhere. Click here to get a copy. (Download)
The Basics of Spanish Vowels
Spanish has five vowels: a, e, i, o and u. We also have y (called i griega or “Greek i” in Spanish).
Scholars don’t completely agree on whether y is a vowel or not, so depending on the source, you can find it under the vowel list or listed separately as a semi-consonant. For the purposes of this post, we’ll treat it as a vowel.
| Spanish vowel | Examples |
|---|---|
| a | agua (water), amigo (male friend), antes (before) |
| e | este (this/East), enero (January), elemento (element) |
| i | isla (island), independiente (independent), invisible (invisible) |
| o | otro (another), océano (ocean), oscuro (dark) |
| u | uno (one), universidad (university), uvas (grapes) |
| y | rey (king), hoy (today), convoy (convoy) |
As you can see (or hear), Spanish and English vowels are pronounced differently. Even in words that are written exactly the same, they sound different in each language.
And unlike in English, Spanish vowels are always pronounced the exact same way. This video from Butterfly Spanish can help you perfect your pronunciation of Spanish vowels:
Tips for Pronouncing Spanish Vowels
Native English speakers learning Spanish tend to give their “English touch” to Spanish vowels. Many times they even change the sound completely, creating a non-existent word or producing another Spanish word altogether.
Here are some of the most important things to remember in order to improve your pronunciation of Spanish vowels.
1. All Spanish vowels are always pronounced the same way.
It doesn’t matter if the syllable is stressed or not or if the vowel has an accent mark. The sound remains the same.
Their length is also always the same, whether they appear at the beginning or end of a word, between consonants, before a double consonant or anywhere else in the word.
Listen to the following words and pay special attention to the vowels. Try to repeat each word after the native speaker:
| Spanish vowel | Examples |
|---|---|
| a | casa
(house), academia
(academy), abanico
(fan) |
| e | detergente (detergent), especie (species), espejo (mirror) |
| i | misionero (missionary), indigente (indigent), difícil (difficult) |
| o | horóscopo (horoscope), odontólogo (odontologist), tocino (bacon) |
| u | cuscús (couscous), zulú (Zulu), burbuja (bubble) |
2. You must pronounce all the vowels in a word.
And all the letters except h, for that matter. There are no silent vowels in Spanish, except in the case of the exception below. If there’s a vowel in a word, pronounce it:
murciélago (bat), destornillador (screwdriver), ayuntamiento (city council)
There is one exception: If a word contains the letters que, qui, gue or gui, the u is silent:
queso (cheese), pesquisa (inquiry), guerra (war), guisante (pea)
3. Don’t “diphthongize” Spanish vowels.
As stated in point one, each vowel has its own unique sound, and it never changes. Don’t add a different vowel sound to the end of a vowel. For example:
Say no instead of /noh-uh/
Say universidad instead of /ew-nee-ver-see-dad/
Say comer instead of /kow-mer/
4. Always read i as “ee.”
Pronounce it like you would say the ee in “see.” This is true no matter how you would read the word in English:
biografía (biography), micrófono (microphone), wifi (wifi)
5. The vowel u always sounds like “oo.”
This is similar to the u in “brute.” By extension, the diphthong eu is always pronounced as “eh-oo.”
universo (universe), unísono (unison), Europa (Europe)
Pronouncing Spanish Vowel Combinations
Vowels don’t always appear by themselves between consonants. You’ll often find Spanish words that have two or three vowels together in a row. When two or more vowels appear together, we get a diphthong, a triphthong or a hiatus.
Spanish Vowel Diphthongs
Simply put, a diphthong forms when two vowels are combined into a single syllable. The sound begins on the first vowel, and then progressively moves toward the sound of the second vowel. Some examples in English can be found in the words “loud,” “foil,” “boy” and “say.”
Spanish diphthongs can only be formed if we have at least one unaccented weak vowel (i or u) together with another vowel. The pronunciation of the vowels in a diphthong isn’t different from the pronunciation of each vowel separately.
Diphthongs come in many forms. Below you’ll find an alphabetical list of Spanish diphthongs so you can see them in action. Practice saying them out loud and try to come up with more examples if you can.
| Diphthong | Explanation | Examples |
|---|---|---|
| ai/ay | Remember that we are treating y as a vowel in this post, and more precisely as a weak vowel. | bailar
(to dance), aire
(air), vainilla
(vanilla) hay (there is/are), espray (spray), ¡ay! (alas!) |
| au | This diphthong sounds like "ah-oo." | aumento (increase), cautela (caution), auténtico (authentic) |
| ei/ey | Same as with ai/ay, we treat the y as a weak vowel. | peinar
(to comb), reina
(queen), aceite
(oil) rey (king), ley (law), virrey (viceroy) |
| eu | This one sounds like "eh-oo." | deuda (debt), reunión (meeting), neutral (neutral) |
| ia | Never confuse the diphthong ia with the combination ía, which will be dealt with in the hiatuses section. | piano (piano), novia (girlfriend), comedia (comedy) |
| ie/ié | It doesn't matter if the strong vowel (a, e or o) in the diphthong has an accent mark. As long as the weak vowel is unaccented, the diphthong continues to exist. | fiera (wild beast), tierra (land/soil), miércoles (Wednesday) |
| io/ió | Again, this diphthong exists with or without an accent on the o, which is the strong vowel. | avión (plane), diosa (goddess), tedioso (tedious) |
| iu | This and ui are diphthongs formed by the two weak vowels. Since Spanish only has one stressed vowel in each word, this combination will always be a diphthong no matter what, because each time the second weak vowel will be unstressed. | viuda (widow), ciudad (city), diurno (daytime [adjective]) |
| oi/oy | These both sound like "oh-e," similar to the sound of "oy" in the English word "boy." | boina
(beret), heroico
(heroic), estoico
(stoic) hoy (today), soy (I am), voy (I go/I'm going) |
| ou | There are only a few words in Spanish containing the diphthong ou, and almost all of them were borrowed from other languages. | Lourdes ([female name]), gourmet (gourmet), soufflé (soufflé) |
| ua | This one sounds like "oo-ah." | agua
(water), cuatro
(four), actuar
(to act) |
| ue | This one makes a "oo-eh" sound. | fuego (fire), acuerdo (agreement), bueno (good) |
| ui/uy | This is the other combination of two weak vowels, and as with iu, it will always form a diphthong no matter what. | circuito
(circuit), juicio
(trial), intuir
(to sense) muy (very), ¡uy! (oh!/ow!), cuy (guinea pig) |
| uo | This one sounds like "oo-oh." | antiguo (ancient), monstruo (monster), residuo (residue) |
Spanish Vowel Triphthongs
Now that we know all the possible diphthong combinations in Spanish, let’s have a look at triphthongs. Triphthongs are formed when we have three consecutive vowels in the same syllable, if and only if:
1. The two outer vowels are weak (i.e. i or u)
2. The central vowel is strong (i.e. a, e or o)
3. None of the weak vowels are accented
If these three rules are observed, we have a triphthong. Triphthongs are way less common than diphthongs in Spanish, and even though there’s a variety of them, the same small group tends to appear more often than the rest.
When pronouncing a triphthong, pronounce the three vowels in order of appearance, stressing the middle one. Here are a few examples:
| Triphthong | Explanation | Examples |
|---|---|---|
| iai/iái | As with most of the Spanish triphthongs, this one normally appears in conjugated verbs. In this case, it's most often seen in the second person plural of the present indicative and the present subjunctive. | liais
(you all roll), riais
(that you all laugh, subjunctive) cambiáis (you all change), aspreciáis (you all appreciate) |
| iei/iéi | These combinations are present mainly in the second person plural of the present indicative and the present subjunctive. | lieis
(that you all roll [subjunctive]), guieis
(that you all guide, subj.) cambiéis (that you all change, subj.), apreciéis (that you all appreciate, subj.) |
| uay/uái | Here we have a mix of nouns, adjectives and the second person plural of the present tense. | Uruguay
(Uruguay), Paraguay
(Paraguay), ¡guay!
(cool!) averiguáis (you all find out), apaciguáis (you all appease) |
| uéi/üéi | These are mainly present in the second person plural of the present subjunctive of the verbs included in the group above. | averigüéis (that you all find out, subj.), apacigüéis (that you all appease, subj.), habituéis (that you all get used to, subj.) |
| Other | There are other triphthongs in the Spanish language, but they aren't so common as to create a group with them. Here are a few with some examples. | uey: buey
(ox) uau: guau (wow/woof) iau: biaural (binaural) |
Spanish Vowel Hiatuses
A hiatus is basically the opposite of a diphthong and exists when two vowels are together but they belong to two separate syllables. Consecutive vowels can be in two syllables because the vowels are both weak or strong, or because the weak vowel is the stressed one in the word.
Once again, the pronunciation of these vowels is invariable, no matter which letter carries the stress. To pronounce hiatuses correctly, you simply read them as they’re written. For example, in the word había we pronounce the stressed i and then the a, so it sounds like “ah-bee-a” (stress on bee).
Hiatuses can be divided into several types, but in order to simplify things, we’ll use a broad division consisting of only two groups:
1. Simple hiatuses
These consist of two strong vowels or two weak vowels:
| Hiatus | Examples |
|---|---|
| aa | Aarón (Aaron), azahar (orange blossom) *Remember that the h is silent, so we pretend it's not there. |
| ae/aé | caer (to fall), caerá (he/she/it will fall), aéreo (aerial) |
| ao/aó | caoba (mahogany), cacao (cocoa), caótico (chaotic) |
| ea | fea (ugly, feminine), azotea (rooftop), berrear (to howl/to scream) |
| ee | creer (to believe), dehesa (meadow/pasture), poseer (to possess) |
| eo/eó | feo
(ugly, masculine), ateo
(atheist), teórico (theoretical) |
| ii/ií | friísimo (very cold), antiinflamatorio (anti-inflammatory) |
| oa | koala (koala), loar (to praise), anchoa (anchovy) |
| oe/oé | áloe (aloe), héroe (hero), coetáneo (contemporary) |
| oo/oó | cooperación (cooperation), zoológico (zoo), loó (he/she/it praised) |
| uu | duunvirato (duumvirate) |
2. Accentual hiatuses
These occur when one of the weak vowels of what was supposed to be a diphthong is accented. The stressed vowel will always have an accent mark in order to signal that the diphthong has been broken:
| Hiatus | Examples |
|---|---|
| aí | ahínco (vigor), país (country), judaísmo (Judaism) |
| aú | baúl (trunk/chest), ataúd (coffin), aún (still/yet) |
| eí | cafeína (caffeine), increíble (incredible), proteína (protein) |
| eú | reúne (he/she/it gathers), transeúnte (passer-by), feúra (ugliness) |
| ía | The imperfect tense of all -er and -ir verbs: comía (I/he/she/it used to eat/was eating) había (there was/used to be) conocíamos (we know/used to know) |
| íe | Many verbs in the 2nd and 3rd person of the present tense and the 2nd and 3rd person of the present subjunctive: te ríes (you laugh) se ríe (he/she/it laughs) críes (that you raise, subjunctive) |
| ío | río (river), mío (mine), crío (kid) |
| oí | arcoíris (rainbow), oído (ear), egoísta (selfish) |
| úa | All verbs ending in -uar in the 2nd and 3rd person singular and the 3rd person plural of the present tense: evalúas (you elevate) actúa (he/she/it acts) continúan (they/you all continue) |
| úe | All verbs ending in -uar in all the persons except the 1st and 2nd plural of the present subjunctive: evalúes (that you elevate, subj.) actúe (that he/she/it acts, subj.) continúen (that they/you all continue, subj.) |
| úo | All verbs ending in -uar in the 1st person singular of the present tense: evalúo (I evaluate) insinúo (I imply/insinuate) actúo (I act) |
This post contains a lot of information, but don’t get overwhelmed! Just try to learn the few rules presented and use the examples for practice.
To get used to them, listen to vowels in context. Spanish music, movies and other audio or video resources are a great way to get exposed to Spanish vowels.
Language learning programs with multimedia features can also help familiarize you with vowels and proper enunciation. For example, FluentU lets you listen to and learn from short Spanish videos equipped with interactive subtitles.
FluentU takes authentic videos—like music videos, movie trailers, news and inspiring talks—and turns them into personalized language learning lessons.
You can try FluentU for free for 2 weeks. Check out the website or download the iOS app or Android app.
P.S. Click here to take advantage of our current sale! (Expires at the end of this month.)
Download: This blog post is available as a convenient and portable PDF that you can take anywhere. Click here to get a copy. (Download)
And One More Thing…
If you've made it this far that means you probably enjoy learning Spanish with engaging material and will then love FluentU.
Other sites use scripted content. FluentU uses a natural approach that helps you ease into the Spanish language and culture over time. You’ll learn Spanish as it’s actually spoken by real people.
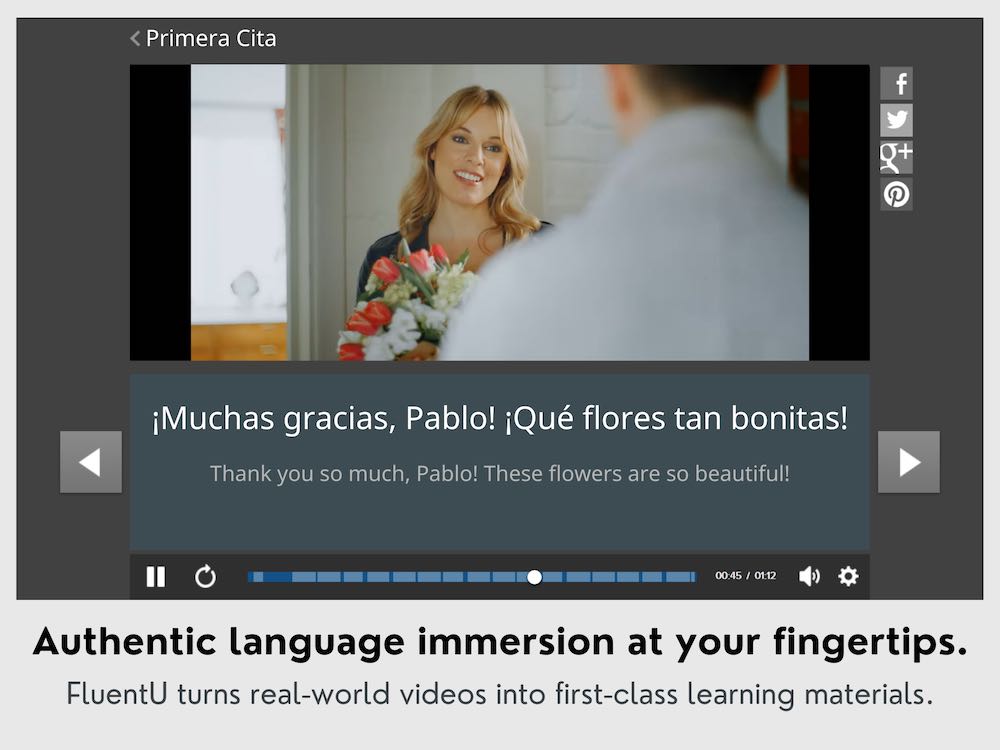
FluentU has a wide variety of videos, as you can see here:
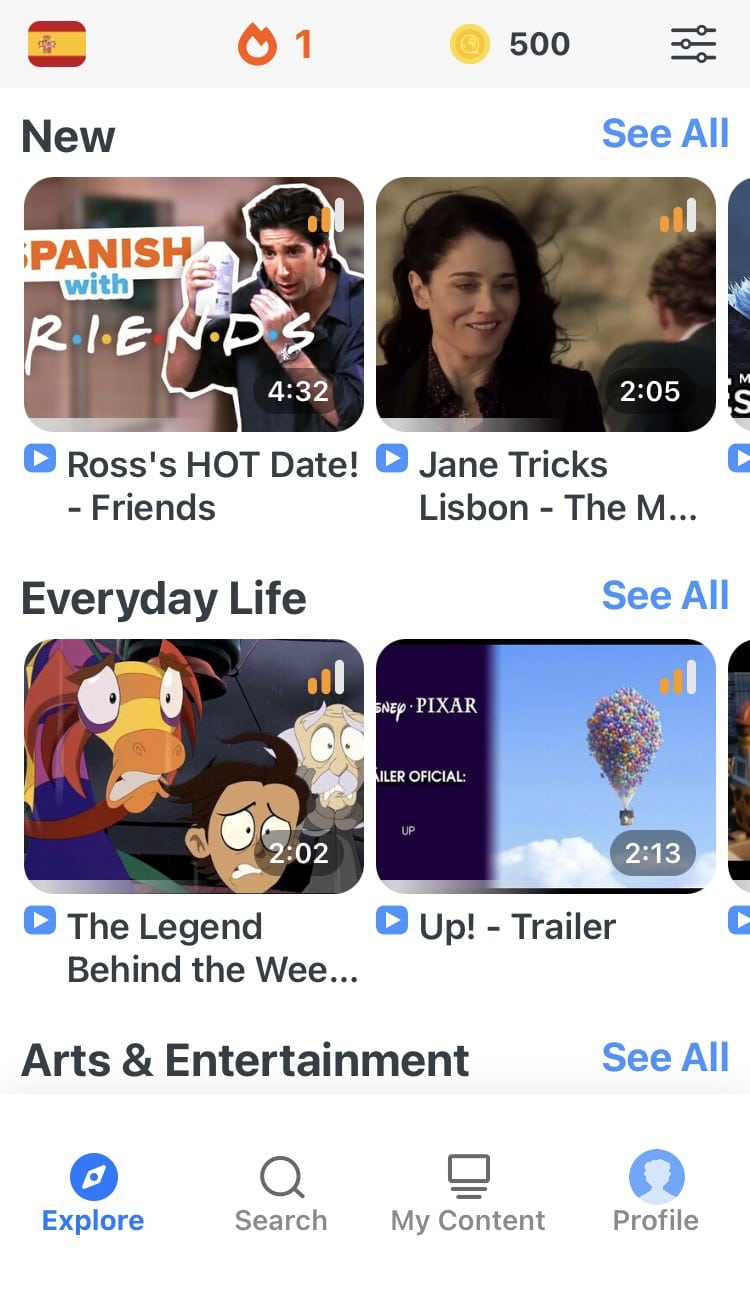
FluentU brings native videos within reach with interactive transcripts. You can tap on any word to look it up instantly. Every definition has examples that have been written to help you understand how the word is used. If you see an interesting word you don’t know, you can add it to a vocab list.
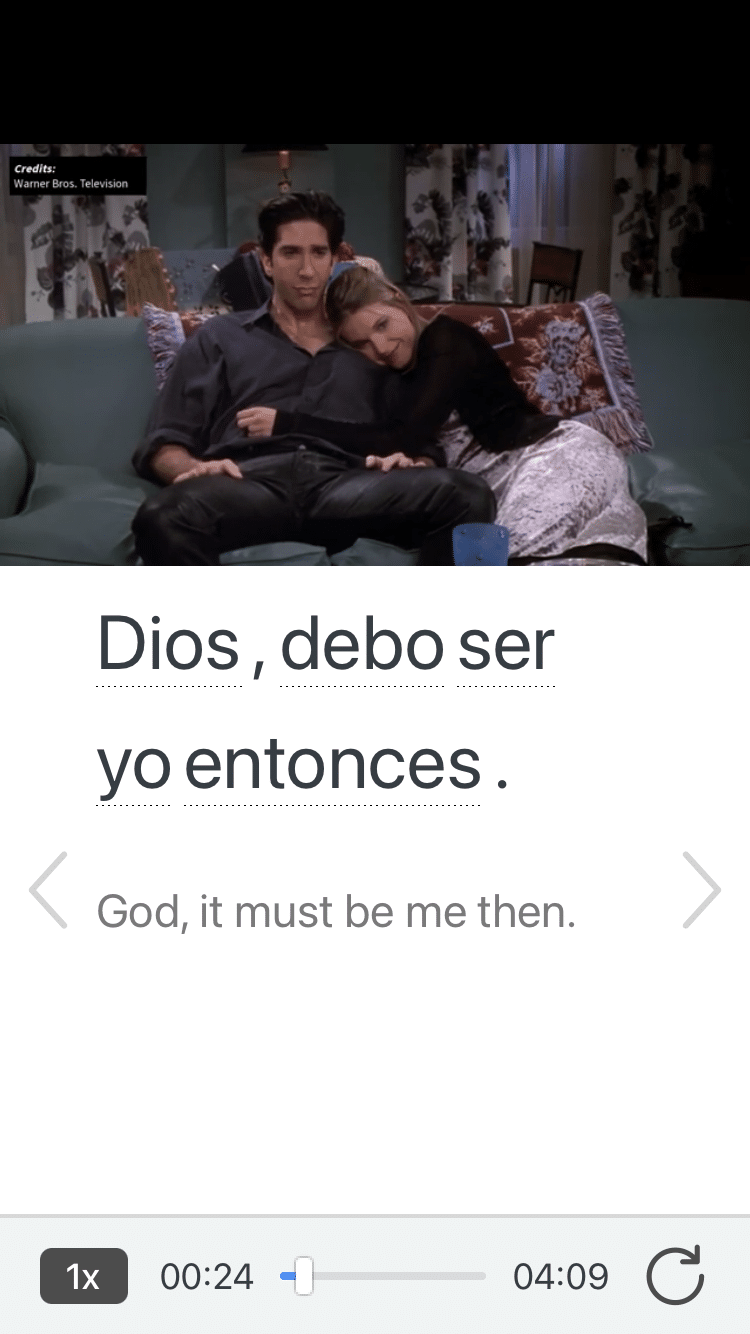
Review a complete interactive transcript under the Dialogue tab, and find words and phrases listed under Vocab.
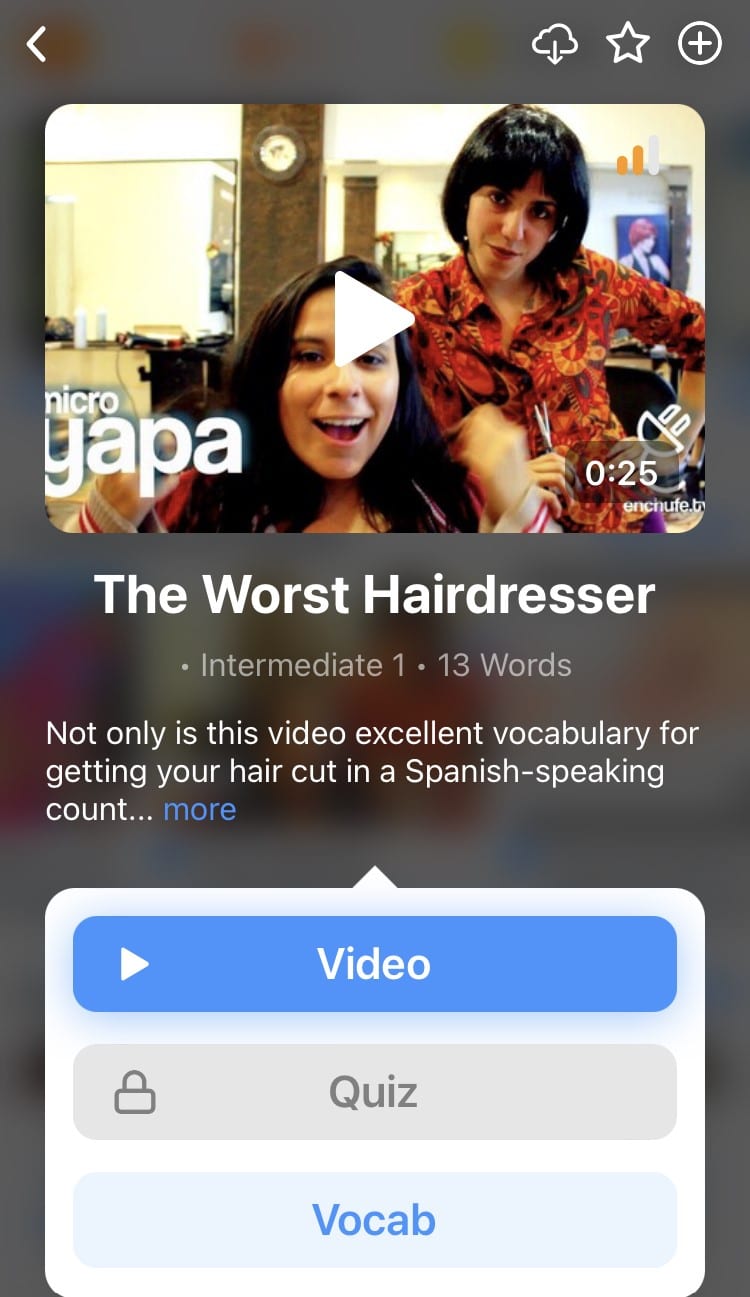
Learn all the vocabulary in any video with FluentU’s robust learning engine. Swipe left or right to see more examples of the word you’re on.
The best part is that FluentU keeps track of the vocabulary that you’re learning, and gives you extra practice with difficult words. It'll even remind you when it’s time to review what you’ve learned. Every learner has a truly personalized experience, even if they’re learning with the same video.
Start using the FluentU website on your computer or tablet or, better yet, download the FluentU app from the iTunes or Google Play store. Click here to take advantage of our current sale! (Expires at the end of this month.)