20 French Conjunctions
Conjunctions are important to make your sentences connect and make sense when they’re more complex. And French requires a lot of them!
In this post, we’ll look at three types of French conjunctions: coordinating, correlative and subordinating.
By the end, you’ll know how to use each type of conjunction and understand why conjunctions are so important to the soul of the French language.
Contents
- What Is a Conjunction?
- French Coordinating Conjunctions
- French Correlative Conjunctions
- French Subordinating Conjunctions
- French Conjunctions Practice Quiz
- And one more thing...
Download: This blog post is available as a convenient and portable PDF that you can take anywhere. Click here to get a copy. (Download)
What Is a Conjunction?
A conjunction is a word that joins together two or more clauses into one sentence (or, minimally, two or more words together into a phrase). In English, this includes words like “and,” “or,” “then” and “since.”
The same sorts of words serve as conjunctions in French as well. Conjunctions are divided into three types: coordinating, correlative and subordinating.
Now we’ll define each of these types, and demonstrate specific conjunctions from each one!
French Coordinating Conjunctions
A coordinating conjunction is used to combine two equal words or clauses, where neither word or clause relies on the other.
For example, here is the coordinating conjunction “and” combining two equally important words:
“Sarah likes books and hot chocolate.”
There are ten coordinating conjunctions in French: car (because), parce que (because), or (but/yet), ensuite (then), et (and), ou (or), ou bien (or), puis (then), mais (but) and donc (therefore/so).
1. Car — Because
Car means “because” but it is used more in writing than in everyday conversation.
Example: Il mange car il a faim. (He’s eating because he’s hungry.)
2. Parce que — Because
Though parce que (because) has a few subtle differences from car (because), it has become nearly the same in meaning and use.
Parce que is typically spoken whereas car is typically written.
Example: Il mange parce qu’il a faim. (He’s eating because he’s hungry.)
3. Or — But / yet
Though many websites will say that or means “now,” it’s more often used to mean “but” or “and yet” when used as a conjunction.
Example: Il faudrait arriver au travail avant 8h30, or, il y a trop de traffic. (It’s required to be at work before 8:30, but/and yet, there’s too much traffic.)
4. Ensuite — Then
When used as a French coordinating conjunction, ensuite (then) is typically preceded by another conjunction, et (and), as seen above. They are, however, two separate conjunctions.
Example: Je vais aller au travail et ensuite au magasin. (I’m going to go to work and then to the store.)
5. Et — And
Et (and) is one of the most common coordinating conjunctions and is used to join two sentences or words together.
Example: J’aime ma maman et mon papa. (I love my mom and my dad.)
It can also be used to combine two separate clauses:
Example: J’aime ma maman et j’adore mes amis. (I love my mom and I really like my friends.)
6. Ou — Or
Ou (or) is another common French conjunction that allows a speaker to provide two options of equal importance.
Example: Veux-tu un verre du vin ou une baguette… ou peut-être les deux ? (Do you want a glass of wine or a baguette… or perhaps both?)
Note: This is not to be confused with où, which means “where” and is distinguished by an accent grave (grave accent).
7. Ou bien — Or else / otherwise
This one can be tricky to master: In most resources you’ll find the translation for ou bien as “or else,” however in practical use, I’ve found that it more often means something closer to “or otherwise” (as in the example below).
This is particularly true since the English phrase “or else” can have a threatening connotation which it doesn’t have in French.
Example: Vous pouvez utiliser une carte de crédit, ou bien, nous acceptons aussi les chèques. (You can use a credit card, or otherwise, we’ll also accept checks.)
8. Puis — Then
Puis (then) is nearly synonymous with ensuite (then), though there is an important difference!
Puis is strictly used as a conjunction to join two sentences together and can never be placed at the end of a phrase.
Example: Je me suis habillé, puis je suis allé dehors. (I got dressed, then I went outside.)
Ensuite, however, can be used as a conjunction (as seen above) but can also be used as an adverb and placed at the end of a sentence.
For example, you can say, “Qu’est-ce qu’il a fait ensuite ?” (“What did he do then/next?”), but you can never say, “Qu’est-ce qu’il a fait puis ?”
9. Mais — But
This French conjunction simply means “but” and is used just as in English: when you have two equal clauses but the second phrase adds information that contradicts the first.
Example: Je veux aller au spectacle, mais je n’ai pas assez d’argent. (I want to go to the concert, but I don’t have enough money.)
10. Donc — Therefore / so
Donc (therefore/so) connects two related clauses and shows a cause and effect. In other words, X is true donc (therefore) Y is true.
Example: J’ai fait le ménage, donc je peux aller au cinéma. (I cleaned so I can go to the movies.)
French Correlative Conjunctions
In some cases, you can join coordinating conjunctions to expand your ideas and express even more complex thoughts.
Below is a list of French correlative conjunctions.
11. Ou… ou — Either… or
You can also use ou bien… ou bien (or… or), though the simple ou… ou construction is most typically heard in spoken French.
Example: Vous avez deux choix pour les desserts, ou (bien) du gâteau ou (bien) de la crème brûlée. (You have two choices for dessert, either cake or crème brûlée.)
12. Ni… ni — Neither… nor
This French conjunction is used in exactly the same way as you would say “neither… nor” in English.
Example: Ni lui ni elle m’aime trop. (Neither he nor her like me very much.)
Though ni isn’t technically considered a coordinating conjunction (although it’s sometimes improperly used that way), it’s a powerful tool when expressing multiple things in the negative.
13. Soit… soit — Either… or
This combined conjunction is nearly identical to ou… ou, and is regularly used in spoken French. However, soit… soit is arguably preferable in French writing.
Example: Il faut choisir soit le rouge soit le bleu. (You need to choose either red or blue.)
French Subordinating Conjunctions
Sometimes when you want to join two phrases together, one of your clauses is entirely dependent on the other (hence why it’s formally known as a “dependent clause”).
For example:
“I’ll give you a ride to the grocery store if you give me $5.”
In this case, the second part creates a condition to the main clause, so we use the appropriate conjunction “if.”
There are many other instances where you would want to join two unequal phrases. Let’s take a look at them in French.
14. Que — That
This French conjunction is incredibly common. It introduces a second clause that compliments the first or adds some necessary information to the main clause.
It’s most often translated as “that” in English, as in “I think that…” or “It’s a good thing that…” and is used as a segue into a dependent clause.
Example: Je pense que finalement il ne viendra pas. (I think that, in the end, he isn’t going to come.)
15. Lorsque — When
This French conjunction comes from the phrase lors que (once) and has come to mean “when.” You typically won’t hear lors que in everyday conversation, as it’s more formal.
Example: Je fais toujours mes devoirs le vendredi soir lorsque je veux sortir le samedi. (I always do my homework on Friday night when I want to go out on Saturday.)
16. Quand — When
Another conjunction meaning “when,” quand is more popularly used than lorsque (when). The two are practically interchangeable but, honestly, you’re always safer to stick with quand.
Example: Je nageais beaucoup quand j’étais jeune. (I swam a lot when I was young.)
17. Comme — Like / as / since
Comme (like/as/since) is used to compare two things or to indicate the cause of something. Above, it’s used in the comparative form, but consider the following sentence indicating causality:
Comme elle a beaucoup d’argent, elle peut acheter n’importe quoi. (Since she has lots of money, she can buy anything.)
In this example, the fact that she has lots of money results in (or causes) the fact that she can buy anything.
More often than not, however, comme will be used as a comparison, as seen in the example below.
Example: Ses yeux brillaient comme des diamants. (Her eyes shine like diamonds.)
18. Puisque — As / since
Similar to comme (like/as/since), puisque also means “as/since.” However, it’s strictly used to indicate cause. Oftentimes, puisque can be translated more loosely as “because” in English, but the formal use and definition is “since.”
Example: Mon ami est allé au restaurant puisqu‘il avait faim. (My friend went to the restaurant since he was hungry.)
Keep in mind that you can also start a sentence with puisque, making the above example look like this:
Puisqu‘il avait faim, mon ami est allé au restaurant. (Since he was hungry, my friend went to the restaurant.)
19. Si — If
Si (if) is used to indicate a condition, meaning that the main clause will only be true if the dependent clause is true.
It functions in the exact same way that the word “if” does in English.
Example: Je t’aiderai si tu m’aides avant. (I can help you if you help me first.)
20. Quoique — Even though
Quoique (even though) is a conjunction that joins two related but opposing ideas.
In the example below, you have the main clause (that you wake up early) and the secondary clause which goes against the first (that you would prefer to sleep later).
Example: Je me lève vers 5h00 le matin quoique je préfère dormir plus. (I wake up at 5:00 in the morning even though I prefer to sleep longer.)
Quoique is a slightly shorter equivalent to malgré que (despite the fact that).
FluentU takes authentic videos—like music videos, movie trailers, news and inspiring talks—and turns them into personalized language learning lessons.
You can try FluentU for free for 2 weeks. Check out the website or download the iOS app or Android app.
P.S. Click here to take advantage of our current sale! (Expires at the end of this month.)
French Conjunctions Practice Quiz
Now it’s time to put all this vocab into practice! Replace the English word in bold with a French conjunction, and check your answers at the end.
1. Je vais aller au supermarché (and) acheter des pommes. (I’m going to go to the grocery store and buy some apples.)
2. J’allais cuire un gâteau (but) je n’ai pas trouvé de farine. (I was going to bake a cake but I couldn’t find any flour.)
3. Je me suis fait beaucoup d’amis (when) je suis allé en Australie. (I made a lot of friends when I went to Australia.)
4. (Neither) Pierre (nor) Marion ne veulent venir à Paris avec nous. (Neither Pierre nor Marion want to come to Paris with us.)
5. Dis-moi (if) tu as besoin d’aide. (Tell me if you need any help.)
6. Je ne vais pas aller à la gym (because) j’ai un examen demain. (I’m not going to go to the gym because I have an exam tomorrow.)
7. Je vais passer un mois au Costa Rica et (then) un mois au Mexique. (I’m going to spend a month in Costa Rica and then a month in Mexico.)
8. Veux-tu partir en Italie (or) en Espagne cet été ? (Do you want to travel to Italy or Spain this summer?)
9. Il est allé à Monaco, (then) il a voyagé en Italie. (He went to Monaco, then he traveled to Italy.)
10. (As) ils ont amené leur chien, ils ne peuvent pas entrer à l’hôpital. (As they have brought their dog, they can’t enter the hospital.)
Answers:
1. et
2. mais
3. quand
4. Ni… ni
5. si
6. parce que
7. ensuite
8. ou
9. puis
10. Comme
Modern French conjunctions are an essential part of sounding like a native speaker.
The best way to pick up on French conjunctions is to hear them used in context by native speakers—pay attention to how they’re used to make ideas and sentences flow together.
If you don’t have any native speakers to chat with, you can watch French videos on YouTube.
But overall, the more you understand how to use French conjunctions, the more fluent you’ll sound.
So keep up the practice, and good luck!
Download: This blog post is available as a convenient and portable PDF that you can take anywhere. Click here to get a copy. (Download)
And one more thing...
If you like learning French on your own time and from the comfort of your smart device, then I'd be remiss to not tell you about FluentU.
FluentU has a wide variety of great content, like interviews, documentary excerpts and web series, as you can see here:
FluentU brings native French videos with reach. With interactive captions, you can tap on any word to see an image, definition and useful examples.
For example, if you tap on the word "crois," you'll see this:
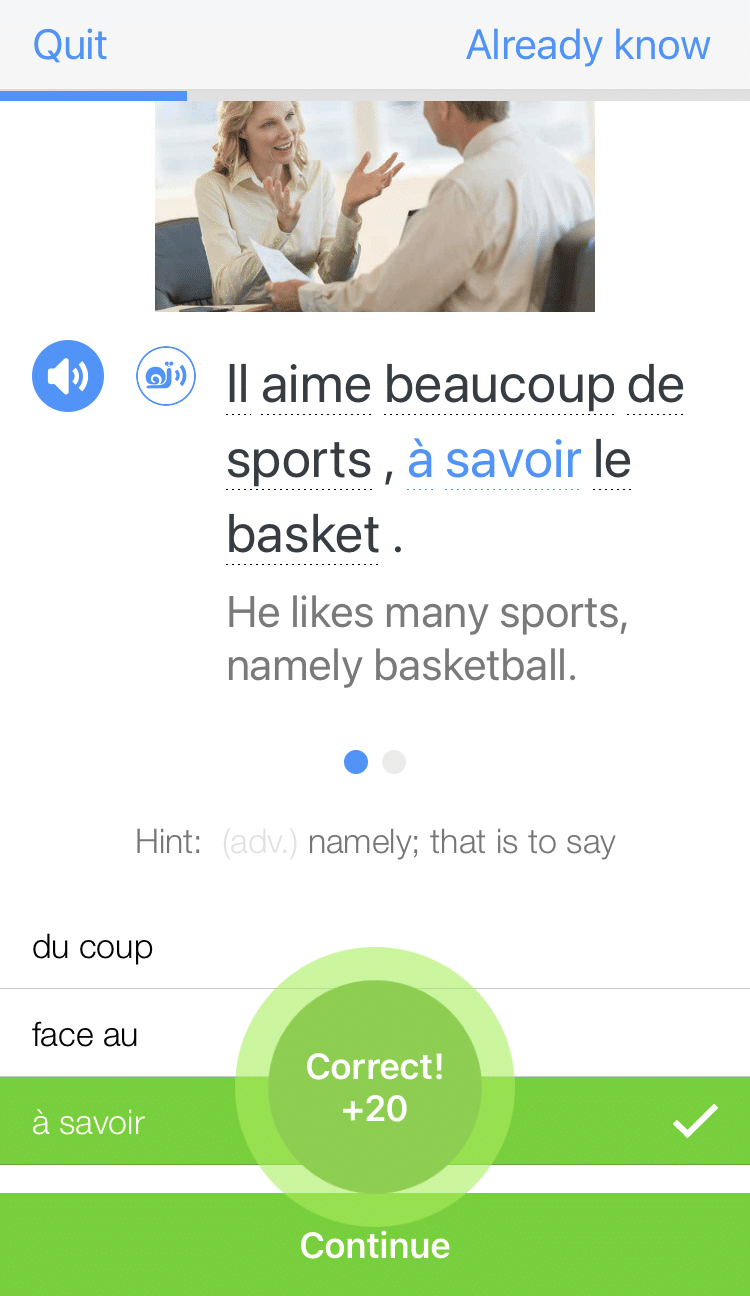
Practice and reinforce all the vocabulary you've learned in a given video with learn mode. Swipe left or right to see more examples for the word you’re learning, and play the mini-games found in our dynamic flashcards, like "fill in the blank."
All throughout, FluentU tracks the vocabulary that you’re learning and uses this information to give you a totally personalized experience. It gives you extra practice with difficult words—and reminds you when it’s time to review what you’ve learned.
Start using the FluentU website on your computer or tablet or, better yet, download the FluentU app from the iTunes or Google Play store. Click here to take advantage of our current sale! (Expires at the end of this month.)